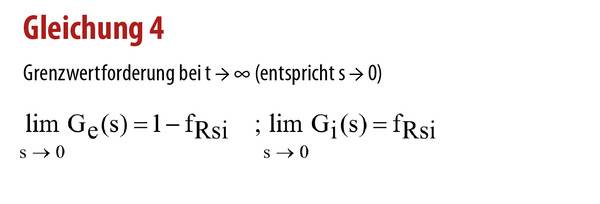Sommerlicher Wärmeschutznachweis nach SKZ-Verfahren

Für den sommerlichen Wärmeschutznachweis muss nach DIN 4108-2 [1] im Sonneneintragsverfahren die Schwere der Bauart bekannt sein. Zur Berechnung der Bauart darf die wirksame Wärmekapazität auch nach DIN EN ISO 13786 [2] für eine Tagesperiode bestimmt werden. In dieser Norm gibt es aber einige Einschränkungen zu beachten:
- Sie gilt nur für sinusförmige Temperaturschwingungen.
- Bestimmte Stoffe, wie beispielsweise Holz oder Porenbeton, werden im vereinfachten Verfahren nach Anhang C eventuell überbewertet.
- Es wird nur die Wärmekapazität auf der Seite des betrachteten Raumes berechnet.
- Laut dem nationalen Vorwort sind die beschriebenen „dynamisch-thermischen Kenngrößen“ für eine thermische Gebäudesimulation nicht anwendbar.
Der Beitrag beschreibt eine Alternative. Für sie gilt:
- Außen- und raumseitige Temperatur eines Bauteils sind innerhalb eines Zeitschrittes konstant.
- Für die Anwendung auf ebene Bauteile mit homogenen Stoffschichten wird von einer eindimensionalen Wärmeleitung ausgegangen. Das Verfahren lässt sich zwar auch auf mehrdimensionale Wärmebrücken anwenden, wofür es aber noch an einer Validierung mangelt.
- Das Verfahren ist nicht auf periodische Vorgänge angewiesen, wodurch es sich als Grundlage für eine thermische Gebäudesimulation eignet. Erweitert kann das Verfahren die dynamische Heiz- und Kühllast beziehungsweise die Ist-Raumtemperatur bei einer Unterdimensionierung der technischen Anlage auch für nicht-adiabate Räume instationär berechnen. Mit unterdimensioniert ist auch gemeint, dass gar keine Heiz- oder Kühlanlage in Betrieb ist, bzw., dass sie nicht nach der Raumtemperatur geregelt wird.
Das SZK-Verfahren für Bauteile
Das Simulationsverfahren mit der Summenzeitkonstante (SZK) wurde bereits in [3] angewendet. Dort wurde aber die Summenzeitkonstante für Aktionen eingesetzt, die sich auf den gesamten Raum beziehen. Inzwischen ist die Erkenntnis gereift, dass man das SZK-Verfahren auf die einzelnen Bauteile eines Raumes ansetzen sollte.
Ausgangspunkt dieser Betrachtung ist daher die Berechnung der raumseitigen Oberflächentemperatur eines Bauteils. Im stationären Fall gilt die Gleichung 1. Der fRsi-Wert ist im Zusammenhang mit Wärmebrückenberechnungen bekannt, kann aber auch für ebene Bauteile verwendet werden. Dafür gilt Gleichung 2. Aus den beiden Faktoren vor der Außen- und Innentemperatur ist zu erkennen, dass es zwei Übertragungsfunktionen mit unterschiedlichen stationären Endwerten geben muss. Für den instationären Fall erhält man im Laplace-Bereich Gleichung 3, mit der Grenzwertforderung (Gleichung 4) zur Sicherstellung des stationären Verhaltens. Damit entspricht auch der Mittelwert von periodischen Vorgängen dem stationären Ergebnis.
Der fRsi-Wert lässt sich Wärmebrückenkatalogen entnehmen oder mit einem Wärmebrückenprogramm berechnen. Nach DIN 4108-2 [1] muss er seit 2003 für Außenbauteile in Neubauten mindestens 0,70 betragen. Das müsste auch für ebene Bauteile gelten, wodurch ein Mindestwert festliegt. Dann geht nach Gleichung 1 die außenseitige Temperatur zu maximal 30 Prozent auf das stationäre Verhalten bzw. auf den zeitlichen Mittelwert der raumseitigen Oberflächentemperatur ein.
Bei den heutigen Anforderungen an den U-Wert von Außenwänden wird der fRsi-Wert in der Größenordnung von 0,97 liegen. Dementsprechend verringert sich der Einfluss der Außentemperatur, wobei allerdings auch eine höhere Amplitude gegenüber der Innentemperatur zu bewerten ist.
Für die beiden Übertragungsfunktionen G(s) soll eine Approximation durch ein Ersatzmodell erfolgen, das möglichst einfache Gleichungen besitzt und die Bedingung in Gleichung 4 erfüllt. Beim Verfahren mit der Summenzeitkonstante wird einfach jede Übertragungsfunktion durch ein Speicherglied erster Ordnung ersetzt und für die Zeitkonstante die Summenzeitkonstante eingetragen. Ein Speicherglied erster Ordnung wird mathematisch durch eine Differentialgleichung erster Ordnung mit konstanten Koeffizienten abgebildet. Für die Simulation ergeben sich daraus für jeden Zeitschritt die einfachen Gleichungen 5 und 6.

Summenzeitkonstante berechnen
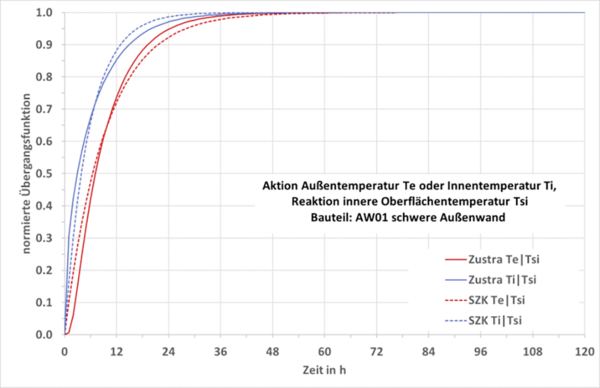
Die Summenzeitkonstante stellt die Summe aller Zeitkonstanten im System dar und kann für ebene Bauteile analytisch aus der sogenannten Kettenmatrix (siehe VDI 6007-1 [5]) oder durch numerische Integration der normierten Übergangsfunktion errechnet werden (Fläche oberhalb der normierten Übergangsfunktion, siehe Abb. 1). Dadurch wird die insgesamt gespeicherte Wärme bei diesem Vorgang berücksichtigt.
Eine Übergangsfunktion h(t) erhält man aus einem Simulationsprogramm beziehungsweise aus einem instationären 2D- oder 3D-Wärmebrückenprogramm, wenn die Aktionsgröße Ti oder Te zum Zeitpunkt t = 0 von 0 auf 1 gesetzt wird und dann konstant bleibt. Alle anderen Aktionsgrößen werden dabei zu Null gesetzt. Die Normierung ergibt sich aus dem Bezug auf den stationären Endwert bei t -> ∞ und dem etwaigen „Durchgriff“ bei t = 0 (Reaktion ohne Zeitverzug bei speicherlosen Bauteilen, Gleichung 7).
Das SZK-Verfahren ist somit wertetreu bezüglich des stationären Verhaltens und der Gesamtwärmespeicherung bei dynamischen Vorgängen. Es berücksichtigt auch eine außenseitige Aktion, die Einfluss auf die raumseitige Oberflächentemperatur nimmt.
Für die Berechnung der beiden Summenzeitkonstanten von ebenen Bauteilen lässt sich das kostenlose Tool „SZKBauteile.exe“ [6] verwenden. Ein Beispiel für die Simulation ist in der Datei „AW08_Ytong-Außenwand mit Außendämmung.xlsx“ in [6] enthalten. In ihr findet sich auch der Vergleich mit dem Simulationsmodell Zustra (siehe unten). Sie kann als Vorlage für eine Validierung verwendet werden. Die Schichtaufbau-
daten der Bauteile in Abb. 2 sind ebenfalls in [6] aufgeführt.
In den folgenden Beispielen für ebene Bauteile wird das grundsätzliche dynamische Verhalten untersucht, das sich durch Variation einiger Parameter ergibt, zum Beispiel die Wirkung und Anordnung einer Wärmedämmung. Die Beispiele sollen Hinweise auf die Größenordnung der Summenzeitkonstante geben und einen Vergleich des Ersatzmodells mit analytisch und numerisch ermittelten Ergebnissen vornehmen.
Übergangsfunktionen verdeutlichen thermisches Verhalten
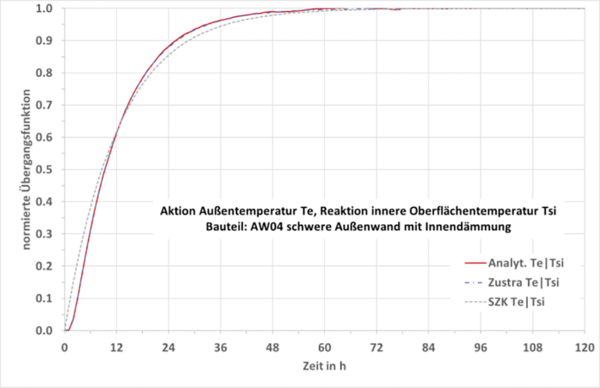
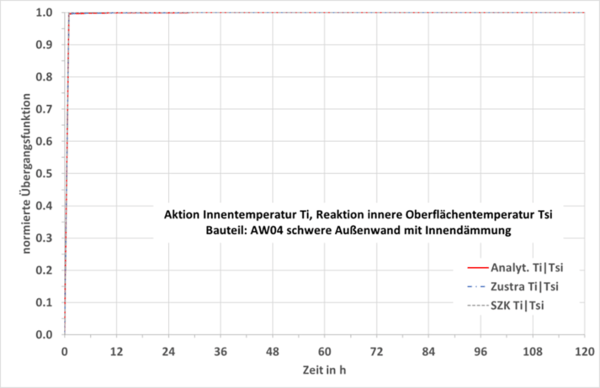
Die auf den stationären Endwert normierte Übergangsfunktion kennzeichnet grafisch das dynamische Verhalten und ist in Abb. 3 und Abb. 4 für eine Außenwand mit Innendämmung und für beide Aktionsgrößen dargestellt. Die rote durchgezogene Linie zeigt die analytische Lösung im Laplace-Bereich durch Multiplikation der Kettenmatrizen und numerische Rücktransformation in den Zeitbereich. Die blaue strichpunktierte Linie ist mit der Zustandsraummethode Zustra berechnet (halbanalytisches Verfahren aus der Systemtheorie, das auch für die thermische Gebäudesimulationen eingesetzt wird). Die grau gestrichelte Linie ist mit dem SZK-Verfahren berechnet.
Man erkennt in Abb. 3, dass erst nach ca. 60 Stunden der stationäre Zustand erreicht wird. Das liegt weit über einer Tagesperiode. Die schnelle Antwort im Abb. 4 stellt keinen Durchgriff dar. Sie resultiert daraus, dass durch die Innendämmung der Wärmespeicher praktisch abgeschnitten wird. Bei allen Beispielen lagen die roten und blau gestrichelten Linien übereinander, was die sehr gute Eignung der Zustandsraummethode auch für Validierungszwecke belegt. In Abb. 4 liegen alle Linien übereinander, was auch weitgehend für alle Leichtbauteile gilt.
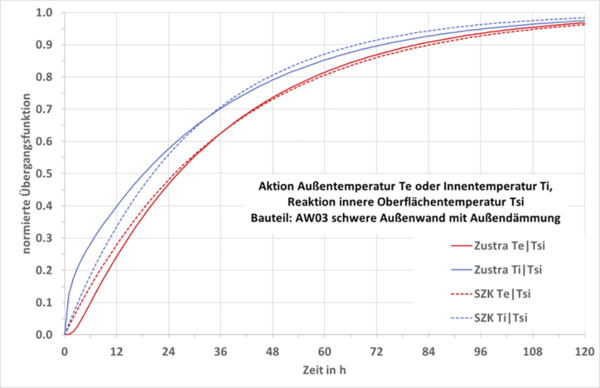
Unterschiede in der Speicherwärme beziehungsweise in den Zeitkonstanten für außen und innen sind auch bei einer schweren Außenwand mit Außendämmung und einer einschichtigen 200mm dicken Betonmauer vorhanden (siehe Abb. 5 und Abb. 6). Die Reaktion auf eine Innentemperaturänderung (blaue Kurven) erfolgt schneller als auf eine Außentemperaturänderung (rote Kurven).
Aus dem Vergleich von Abb. 5 und Abb. 6 lässt sich der Einfluss der Außendämmung ablesen, die sich stark auf das Speicherverhalten der raumseitigen Oberflächentemperatur auswirkt. Die Außendämmung verringert bei der Aktion Ti den Abfluss nach außen, wodurch mehr Wärme gespeichert werden kann. Dagegen wird bei der Aktion Te das Eindringen in das Bauteil verzögert. Das bedeutet für Verfahren, die Schichten auf der gegenüberliegenden Seite vernachlässigen (zum Beispiel [2, Abschnitt C.2.4]), dass sie sich nicht für alle Bauteilaufbauten anwenden lassen. Abb. 2 enthält weitere Beispiele, aus denen man den Einfluss der Schichtaufbauten auf die Summenzeitkonstanten und auf die Stationärwerte entnehmen kann.
In die Außen- und Innentemperatur lässt sich die absorbierte Sonnenstrahlung auf beiden Oberflächen einrechnen, wodurch fiktive Temperaturen für die Berechnung entstehen. Sie wird auch kombinierte oder äquivalente Temperatur genannt. Je nachdem, ob ein Bauteil von außen verschattet wird oder ob die in den Raum transmittierte Sonnenstrahlung hoch oder gering ist, wirkt sie sich unterschiedlich stark auf die fiktiven Temperaturen aus. Dabei handelt es sich um ein grundsätzliches Problem in der DIN EN ISO 13786, wo es darum geht, ob ein Bauteil als schwer oder leicht einzustufen ist. Die Berechnung der Wärmekapazität in dieser Norm geht nur von Schwankungen der Innentemperatur aus, das heißt, von außen betrachtet kann das Bauteil eine ganz andere Wärmespeichereigenschaft bezüglich Tsi aufweisen (siehe Abb. 2).
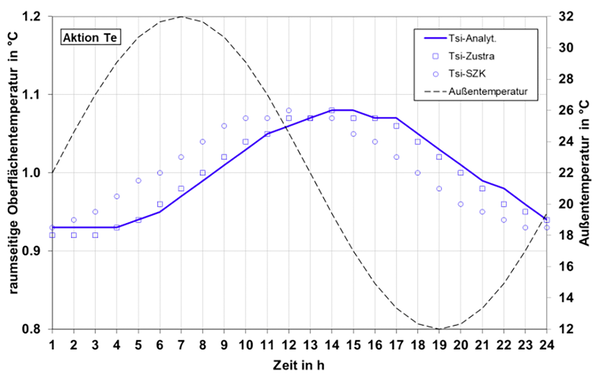
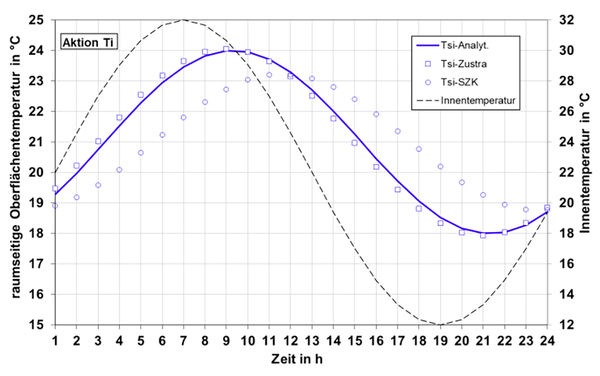
Eine weitere Möglichkeit zur Validierung des Verfahrens bietet der Vergleich mit einem Sinusverlauf für Außen- und Innentemperatur. Periodische Vorgänge lassen sich mit Kettenmatrizen im eindimensionalen Fall analytisch simulieren. Zusätzlich kommt in Abb. 7 und Abb. 8 die Zustandsraummethode Zustra zum Einsatz, um auch dieses Verfahren für die nachfolgende Jahressimulation zu überprüfen.
Die durchgezogenen Linien stellen die analytischen Lösungen für periodische Schwingungen dar. Die Quadrat-Symbole der Zustandsraummethode schmiegen sich dem analytischen Verlauf an. Der Tsi-SZK-Verlauf zeigt eine größere Abweichung vom analytischen Ergebnis, vor allem bei der Aktion Innentemperatur, die allerdings eine sehr große Amplitude aufweist.
Simulationen beweisen Tauglichkeit des Verfahrens
Die folgenden Simulationen zeigen Ergebnisse mit vorgegebenen Außen- und Innentemperaturen. Für die Außentemperaturen kommen zwei Variationen zur Anwendung: eine extrem kalte Winterperiode und ein Jahr mit hohen Außentemperaturen. Die Innentemperaturen in der Jahressimulation werden aus der raumseitigen Randbedingung der DIN 4108-3 [7, Bild D.1] gebildet. Innentemperaturen in der Heizzeit werden dadurch automatisch auf konstante 20 °C gesetzt.
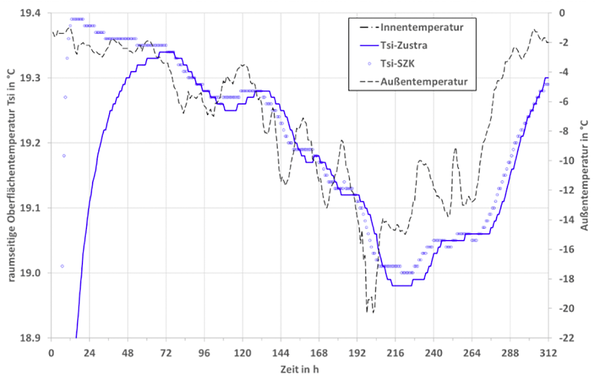
In den ersten Tagen der kalten Periode in Abb. 9 wirkt noch der Startwert, der auf 0 °C gesetzt wurde. Bei dieser Anlaufrechnung ist ein Vergleich mit den numerisch ermittelten Werten aus der Zustandsraummethode erst nach drei bis vier Tagen sinnvoll. Der Kurvenvergleich zwischen Tsi-Zustra und Tsi-SZK zeigt, dass das SZK-Verfahren etwas zu schnell auf die Aktion Außentemperatur reagiert. Dies wurde auch in anderen Beispielen beobachtet, sobald die Summenzeitkonstante einen hohen Wert annimmt. Trotzdem weisen die Abweichungen nur Werte unter 0,1 Kelvin auf.
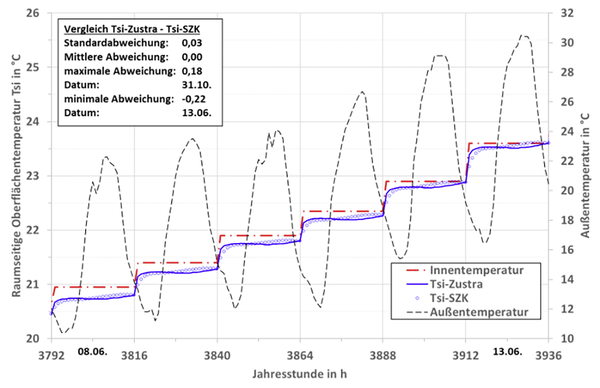
Abb. 10 zeigt einen Ausschnitt der Ergebnisse einer Jahressimulation. Im Zeitraum vom 8.6. bis 13.6 verändert sich auch die Innentemperatur gemäß DIN 4108-3 (rot strichpunktierte Linie) mit dem exponentiell gewichteten gleitenden Tagesmittelwert der Außenlufttemperaturen nach DIN EN 15251 [8]. Auch hier zeigt sich ein Phasenfehler, der aber zu sehr geringen Abweichungen führt. Die betragsmäßig maximale Abweichung liegt über das gesamte Jahr bei 0,22 Kelvin.
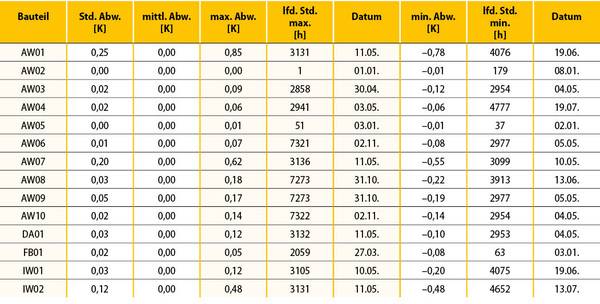
Abb. 11 gibt einen Überblick über die Abweichungen des SZK-Verfahrens von der Zustandsraummethode für die Bauteile aus Abb. 2. Nur die beiden Bauteile AW01 und AW07 mit den hohen U-Werten weisen eine Standardabweichung größer gleich 0,2 Kelvin auf. Alle anderen Bauteile passen sich hervorragend mit einer minimalen Abweichung von -0,22 Kelvin bei AW08 an. Die mittlere Abweichung beträgt aufgrund der oben genannten Wertetreue in allen Fällen 0,00 Kelvin.
Ausblick: SKZ-Verfahren lässt sich erweitern
Das SZK-Verfahren für einzelne Bauteile lässt sich auf ein Raummodell bestehend aus ebenen Bauteilen erweitern, wenn man die Innentemperatur durch eine thermische Umgebungstemperatur ersetzt. Die thermische Umgebungstemperatur sorgt für die getrennte Berechnung der Konvektion mit Lufttemperatur und des langwelligen Strahlungsaustausches der Raumflächen untereinander mit den raumseitigen Oberflächentemperaturen.
Denkbar ist aber auch, auf die getrennte Strahlungs- und Luftankopplung zu verzichten und weiterhin mit der Innentemperatur unter Einschluss der kurzwelligen Strahlungsabsorption wie oben angegeben zu rechnen. Die Heizlastberechnung nach DIN/TS 12831-1 [9] folgt diesem Ansatz, jedoch ohne kurzwellige Strahlungsabsorption. Eine Begründung könnte sein, dass durch eine Möblierung der Strahlungsaustausch zwischen den raumseitigen Bauteiloberflächen behindert wird und somit nicht in der Planung erfassbar ist. Ob ein solch vereinfachtes Raummodell ausreicht, müssten Vergleichsrechnungen mit Simulationsprogrammen beantworten.
Die Weiterentwicklung des SZK-Verfahrens zu einem Raummodell würde auch dem Nachteil des 2K-Modells der VDI 6007-1 begegnen, dass nur adiabate Räume berechnet werden können. In einem Raummodell nach dem SZK-Verfahren kann nicht nur für jedes einzelne Bauteil eine außenseitige Temperatur angegeben werden, es kann auch ein zusammenhängender Bereich mit mehreren Räumen in einem Rechenschritt innerhalb eines Zeitschrittes gelöst werden.
Gibt man eine Innentemperatur vor, benötigt man kein Raummodell. Ein einzelnes Bauteil beziehungsweise eine einzelne Wärmebrücke lässt sich dynamisch untersuchen. Eine mögliche Anwendung: die Berechnung der erforderlichen Lüftung, um Schimmelpilz an erdreichberührten Bauteilen zu vermeiden (Kellerlüftung). Mit der Kenntnis der raumseitigen Oberflächentemperatur zu jedem Zeitschritt kann der kritische Feuchtegehalt nach DIN/TS 4108-8 [10, Anhang H] berechnet werden. Er ist Voraussetzung, um den erforderlichen Volumenstrom ermitteln zu können.
Das SKZ-Verfahren und die Baupraxis
Mit dem Summenzeitkonstante-Verfahren (SZK-Verfahren) lässt sich mit nur drei Eingabewerten das dynamische Verhalten eines Bauteils simulieren. Beispiele zeigen, dass eine sehr gute Näherung für die raumseitige Oberflächentemperatur von ebenen Bauteilen möglich ist. Zudem eignet es sich für einen größeren Frequenzbereich, weil es den gesamten Speichervorgang betrachtet. Das heißt, das SZK-Verfahren entfaltet seine gute Anpassung besonders bei längeren Zeiträumen mit stark veränderlichen Außenklimadaten, wie beispielweise der Simulation mit TRY-Daten.
Die bisherigen Validierungsnormen geben aber meist nur eine kurze Periode mit sinusförmigem Verlauf vor. Deshalb müssen erst neue Validierungsvorgaben entwickelt werden, um das SZK-Verfahren zu etablieren. Diese Vorgaben sollten zunächst die Validierung einzelner Bauteile enthalten, bevor ganze Räume validiert werden. Dadurch würde das Kernstück der Simulation, die Lösung der Wärmeleitungsgleichung, sachgemäß durch eine beschränkte Zahl an Aktionsgrößen überprüft.
Die Beispiele im Beitrag zeigen, dass eine Außendämmung die Wärmespeicherfähigkeit für raumseitige Temperaturschwankungen erhöhen kann. Somit lässt sich die Auswirkung auf den Raum bezüglich des sommerlichen Wärmeschutzes im Prinzip nicht nur anhand der raumseitigen Bauteilschichten beurteilen. Für ein solches Verfahren müssten Einschränkungen in der Anwendung definiert werden.
In der Baupraxis kommt es vor, dass die Schichtaufbauten in einem frühen Planungsstadium noch nicht bekannt sind. Nur die U-Werte der Außenbauteile lassen sich dem GEG-Nachweis entnehmen. Beim SZK-Verfahren hilft es, wenn man bei Vorabberechnungen für die Außenbauteile nur zwei und für die Innenbauteile nur drei Eingabewerte schätzen muss, anstatt sich komplette Schichtaufbauten auszudenken. Da man mit diesen Werten und einem Raummodell schon simulieren kann, könnte die Einschätzung der Bauartschwere ganzer Räume entfallen (siehe VDI 2078 [11, Abschn. 5.5] und DIN 4108-2 [1, Abschn. 8.3.3]). Die Erfahrung hat gezeigt, dass Räume bei dieser Art der Einschätzung problematisch sind, bei denen die Bauteile unterschiedliche Wärmespeichereigenschaften aufweisen.
Dieser Beitrag von Dipl.-Ing. Norbert Nadler ist zuerst erschienen in Gebäude Energieberater 03/2021. Nadler führt in Oranienburg ein Ingenieurbüro für Heizung, Klima, Sanitär, Solar und thermische Bauphysik.
Literatur
[1] DIN 4108-2:2013-02: Wärmeschutz und Energie-Einsparung in Gebäuden – Teil 2: Mindestanforderungen an den Wärmeschutz, Beuth-Verlag
[2] DIN EN ISO 13786:2018-04: Wärmetechnisches Verhalten von Bauteilen – Dynamisch-thermische Kenngrößen – Berechnungsverfahren, Beuth-Verlag
[3] Nadler, N.: C.A.T.S.-Kühllastberechnung, Validierung des Raummodells anhand der neuen VDI 6007-1, tab 12/2012, S. 42-50, Bauverlag BV GmbH
[4] DIN EN ISO 10211:2018-03: Wärmebrücken im Hochbau – Wärmeströme und Oberflächentemperaturen – Detaillierte Berechnungen, Beuth-Verlag
[5] VDI 6007-1:2015-06. Berechnung des instationären thermischen Verhaltens von Räumen und Gebäuden, Raummodell
[6] SZKBauteile.zip auf www.cse-nadler.de
[7] DIN 4108-3:2018-10: Wärmeschutz und Energie-Einsparung in Gebäuden – Teil 3: Klimabedingter Feuchteschutz – Anforderungen, Berechnungsverfahren und Hinweise für Planung und Ausführung, Beuth-Verlag
[8] DIN EN 15251:2012-12: Eingangsparameter für das Raumklima zur Auslegung und Bewertung der Energieeffizienz von Gebäuden – Raumluftqualität, Temperatur, Licht und Akustik, Beuth-Verlag
[9] DIN/TS 12831-1:2020-04: Verfahren zur Berechnung der Raumheizlast – Teil 1: Nationale Ergänzungen zur DIN EN 12831-1, Beuth-Verlag
[10] DIN/TS 4108-8:2021: Wärmeschutz und Energie-Einsparung in Gebäuden – Teil 8: Vermeidung von Schimmelwachstum in Wohngebäuden, Beuth-Verlag
[11] VDI 2078:1996-07: Berechnung der Kühllast klimatisierter Räume (VDI-Kühllastregeln), Beuth-Verlag