Ansaugen aus der Tiefe: Wie funktioniert eigentlich eine Pumpe?

Um die Zusammenhänge herzustellen, sollte man zuerst sämtliche Daten zur Umgebung einer solchen Tiefenhebung festhalten. Gehen wir also von einem Tag an einem tiefen See mit einer Umgebungs- und Wassertemperatur von ca. 10 °C aus. Der Luftdruck soll genau 1000 Millibar (abgekürzt mbar) betragen. Die umgangssprachliche Erdanziehung soll völlig normal wirken und einen Wert von rund 10 m/s² annehmen. Das spezifische Gewicht von Wasser soll unabhängig von Tabellenwerten mit 1000 Kilogramm je Kubikmeter ausreichend genau berücksichtigt sein. Bleiben wir bei diesen Annahmen und gehen mit gesundem Menschenverstand ohne weitere Tabellenwerte über Wasser und Luft an die Aufgabe heran.

Gedanklich tauchen wir jetzt ein Rohr mit einer Gesamtlänge von 20 Metern in den See. Dieses Rohr ist aus Glas und an einem Ende mit einer Kappe verschlossen. Das andere Ende ist komplett geöffnet. Damit auch die letzte Luftblase aus dem Rohr austritt, wird es mit der Öffnung schräg nach oben unter Wasser gedrückt und erst dann mit der Öffnung nach unten senkrecht in den See eingetaucht. Das Rohr bleibt vollgefüllt mit Wasser (siehe Skizze). Jetzt wird das Rohr Stück für Stück aus dem Wasser herausgezogen. Wie bei einem mit dem Daumen verschlossenen Trinkhalm wird man nun beobachten können, dass das Wasser in dem gläsernen Rohr hängenbleibt. Begründung: Die Kappe verhindert ein Eindringen von Luft, der Bereich zwischen Kappe und Wasser kann als komplett evakuiert angesehen werden.

Nun wird dieses Rohr Meter für Meter immer weiter senkrecht angehoben. Die Säule reißt nicht ab, bis eine Höhe des Rohres von rund zehn Metern erreicht ist. Bei dieser Höhendifferenz zwischen Wasseroberfläche und Oberkante Kappe bleibt die Wassersäule gewissermaßen hängen. Guckt man genau hin, bilden sich Gasblasen an der Oberfläche, kurz unterhalb der Kappe. Einerseits wird das im Wasser enthaltene Gas entweichen. Zusätzlich verdampft das Wasser in diesem obersten Bereich des Glasrohres. Das Wasser in diesem Glasrohr in 10 Metern Höhe über diesem See verdampft bei einer Umgebungstemperatur von 10°C.

Das sagen die physikalischen Gesetze

Egal aus welchem Material dieses Rohr besteht, das Ergebnis lässt sich zigfach wiederholen. Bei einer Wasserhöhe von 10 Metern kocht das Wasser oben im Rohr. Der springende Punkt: Die Wassersäule in diesem gläsernen Rohr kann nicht unterscheiden, ob eine Kappe das Nachströmen von Luft verhindert oder ob eine Pumpe diesen Bereich leer gepumpt bzw. evakuiert hat. Bei 10 Metern Höhe ist Schluss aufgrund physikalischer Gesetze. Der Schweredruck der zehn Meter hohen Wassersäule ergibt sich aus der Formel:

Für die Szene mit dem gläsernen Rohr gilt daher:

Das Wasser übt also, wenn es 10 Meter weit über der Seeoberfläche in dem Glasrohr festgehalten wird, einen Druck von 1000 mbar aus. Und wenn der Umgebungsdruck nun genauso groß ist, also ebenfalls 1000 mbar, halten sich der Luftdruck, der auf die Wasseroberfläche des Sees drückt, und die Wassersäule gerade noch die Waage. Ein weiteres Anheben des Rohres nimmt also die Wassersäule nicht mehr mit in die Höhe, da der Luftdruck als Gegendruck nicht entsprechend ausreicht. Bei diesen schlichten und verkürzten Annahmen beträgt die theoretische Saughöhe einer Pumpe rund zehn Meter.

Wie bereits beschrieben, mehr als ein Vakuum kann auch die beste Pumpe nicht ziehen. Ob die Luft aus der Kappe per Pumpe oder mittels dieser gedachten Versuchsanordnung rausgezogen wurde, ist dem Wasser völlig schnuppe. Es ist auch uninteressant, wie tief das Rohr noch unter Wasser eintaucht. Einzig der Luftdruck entscheidet über die maximale Saughöhe einer Pumpe. Der Luftdruck kann also unter diesen Umständen das Wasser nicht höher als 10 Meter ins Rohr drücken.

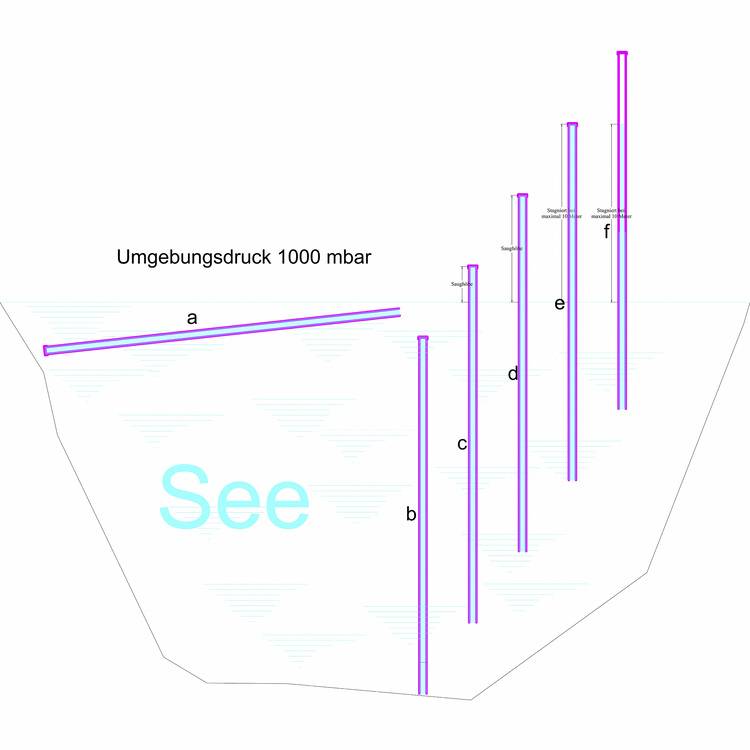
Die Versuchsanordnung:

a) Das untergetauchte Glasrohr wird blasenfrei mit Wasser gefüllt.

b) Das gefüllte Rohr wird senkrecht ins Wasser getaucht.

c, d) Zieht man das Rohr aus dem Wasser, bleibt die Säule unterhalb der Kappe hängen.

e, f) Erst bei einer Anhebung bis und dann über zehn Meter über den Wasserspiegel bleibt die Wassersäule hängen.

Diese Faktoren beeinflussen die reale Saughöhe

Im gerade skizzierten Falle mit dem gläsernen Rohr wurden der Einfachheit halber sehr glatte Annahmen getroffen. Im echten Leben beeinflussen reale Faktoren die echte Saughöhe einer Pumpe jedoch noch erheblich. Nicht jede Pumpe ist von Hause aus geeignet, beliebig niedrige Drücke bereitzustellen. Je nach Konstruktion ist oft ein Unterdruck (physikalisch korrekt: negativer Überdruck) von nur 200 mbar als niedrigster Wert möglich. Die Saughöhe würde dann nur noch acht Meter betragen (1000 mbar – 200 mbar = 800 mbar).

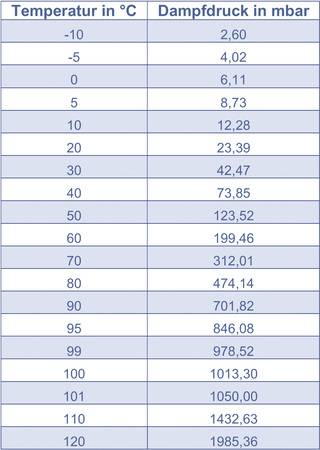
Als weiterer Einfluss variiert die Dichte des Wassers temperaturabhängig. Man müsste daher unterstellen, dass heißes und damit leichteres Wasser ein wenig höher gesaugt werden könnte als kaltes, schwereres Wasser. Diese Logik stimmt nur bedingt. Denn mit zunehmender Temperatur steigt auch die Neigung des Wassers, sich in Dampf aufzulösen. Kaltes Wasser von 20°C verdampft erst bei einem absoluten Druck von rund 18 mbar. Theoretisch könnte eine Pumpe Wasser von 20°C aufgrund dieser Eigenschaft noch 9,82 Meter hoch saugen, bis es dampfförmig wird. Wasser mit einer Temperatur von beispielweise rund 82°C würde bereits bei 500 mbar Druck dampfförmig. Dies entspräche einer theoretischen maximalen Saughöhe von fünf Metern. Annähernd kochendes Wasser von vielleicht 98°C lässt sich nur noch wenige Zentimeter hoch ansaugen, bevor es verdampft.

Der letzte, jedoch sehr geringe Einfluss ist die Änderung der Erdbeschleunigung auf unserer kugeligen Welt. Häufig wird diese mit 9,81m/s² angenommen. Diese Größe verändert sich jedoch, wenn auch nur gering, in Abhängigkeit von Höhenlage und Abstand zum Äquator.

Was, wenn die Praxis anders aussieht?

Es existieren natürlich auch Bohrungen bis in eine Tiefe von 20 Metern und mit einem Ansaugrohr, das in dieser Tiefe endet. Wie kann es sein, dass eine Pumpe aus dieser Tiefe fördert? Dafür kann es zwei Gründe geben:

1. Das Bohrgestänge und auch anschließend das Saugrohr sind tatsächlich auf eine Tiefe von 20 Metern abgesenkt. Der Grundwasserspiegel liegt aber deutlich darüber. Bei dem beispielhaft beschriebenen Glasrohr kann das abgesenkte Rohr ja auch unter Wasser noch (s. Skizze) ganze zehn Meter in die Tiefe reichen. Entscheidend ist die Saughöhe ab Oberkante Wasserspiegel. Egal ob es ein Grundwasserspiegel ist oder die Oberfläche eines Sees.
2. Die Pumpe ist nicht oberirdisch montiert, sondern mit dem wasserfördernden Rohr in die Tiefe abgelassen worden. Ist die Pumpe in 20 Metern Tiefe und dann auch noch mitten im nachfließenden Grundwasser montiert, saugt sie nicht nach oben, sondern drückt das Wasser ans Tageslicht. Das Drücken ist für eine entsprechende Pumpe unproblematisch. Da reißt nichts ab oder verdampft. Druckhöhen von Pumpen sind von der rein physikalischen Seite her erstmal nicht begrenzt.

Die theoretische Saughöhe einer Pumpe wird durch den umgebenden Luftdruck begrenzt und beträgt für Wasser ca. zehn Meter. Praktisch kann diese Saughöhe aber nicht erreicht werden. Kein noch so innovativer Pumpenhersteller kann hier dran etwas ändern. Bei extremem Unterdruck neigt Wasser zur Verdampfung. Auch diese Tatsache begrenzt die praktische Saughöhe einer Pumpe.

So hilft das Venturi-Prinzip

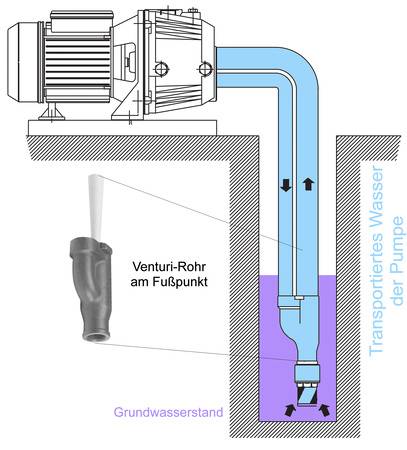
Ein Trick kann dazu führen, dass man die eigentliche Pumpe oberirdisch platziert und doch noch aus Tiefen von mehr als 10 Metern fördern kann. Verfolgen Sie das kurze Gedankenexperiment: Man stelle sich zwei Rohre vor, die in der Tiefe von 20 Metern miteinander verbunden sind. Wie mittels einer Umwälzpumpe könnte man Wasser auf der einen Seite in die Tiefe drücken und gleichzeitig würde es sich an der anderen Seite aus der Tiefe wieder nach oben bewegen. Theoretisch könnte eine Umwälzpumpe aus dem Heizungsbau diesen Kreislauf antreiben.

Kurz überlegt: Mit einem Strömungsabriss aufgrund des Luftdrucks von nur 1000 mbar hat man nichts zu tun. Auch fängt das Wasser nicht an zu kochen, weil die Wassersäule auf beiden Seiten dies verhindert. Die umlaufende Wassermenge könnte man am Fußpunkt, also in 20 Metern Tiefe, durch eine Verengung treiben. In der Folge würde der dynamische Anteil des Drucks zunehmen, der statische Druck abnehmen. Das entspricht dann dem Venturi-Rohr, mit dem man dann an dieser Stelle Wasser ansaugen könnte. Dieser Kreislauf mit Verengung am Fußpunkt in 20 Metern Tiefe würde also theoretisch und praktisch Wasser auch aus dieser Tiefe zu Tage fördern können. Genau genommen würde das Wasser aber hochgedrückt und eben nicht gesaugt.

Zugegeben, diese Technik suggeriert auf den ersten Blick das Aussetzen physikalischer Gesetze. Erst bei näherer Betrachtung erkennt man das Venturi-Prinzip, das Sie sich gerne nochmal im Heft-Archiv vom SBZ Monteur ansehen können. 

Erkenntnisse allgemeiner Art

Wasserpumpen unterliegen üblicherweise dem Zwang, dass diese eben nur Wasser und nicht Dampf oder Luft fördern können. Je nach Bauart sind Pumpen daher auf einen entsprechenden Umgebungsdruck auf der Saugseite angewiesen. Das bedeutet beispielsweise, dass Pumpen und insbesondere deren Laufräder zerstört werden können, wenn ein gewisser Druck auf der Saugseite nicht eingehalten wird. Begründet ist dieses Phänomen mit der Tatsache, dass Wasser in Abhängigkeit von Umgebungsdruck und Temperatur verdampfen kann. Beispielsweise in einer Heizungsanlage mit einer Vorlauftemperatur von 55 °C würde ein Umgebungsdruck von 160 mbar zur Verdampfung führen. Wohlgemerkt 160 mbar als absoluten Druck. Würde dieser Druck an einer Stelle des Pumpenrades unterschritten, würde sich schlagartig Dampf bilden. Das nennt man dann Kavitation. Hersteller von Umwälzpumpen geben einen sogenannten Mindestzulaufdruck für ihre Pumpen an.

Nochmals zurück zum eigentlichen Thema: Die theoretische Saughöhe einer Pumpe wird also auch durch das physikalische Gesetz zum Dampfdruck begrenzt.

Dieser Beitrag ist zuerst erschienen in SBZ Monteur 10/2020.