Basiswissen für Handwerker: Seilkraft

Sei es das Rohr unter der Decke oder die Dachrinne mit Gefälle - es ist extrem hilfreich, wenn Handwerker neben ihrer Alltagserfahrung dieses Gesetz der Statik kennen und anwenden können.

MEFA: Abhängungssystem für Lüftungsrohre — © MEFA

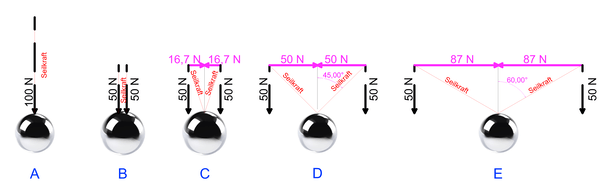
Statik ist ein Teilgebiet der Physik und der Mechanik. Diese beschäftigt sich mit unbewegten Systemen. Und hier gilt eine goldene Regel, die als Gedankenmodell eine sehr einfache Übung darstellt. Als Gleichgewichtsbedingung gilt nämlich, dass die resultierenden Kräfte, die auf einen Körper wirken, gleich Null sein müssen, damit dieser unbewegt bleibt. Im einfachsten Fall hängt also ein Gewicht mit 10 Kilogramm (kg) Masse an einem Seil und befindet sich erst dann in Ruhe, wenn dieses Seil der Gewichtskraft eine gleichgroße Gegenkraft entgegensetzt. Die Gewichtskraft der Masse von 10 kg entspricht ungefähr 100 Newton (N). Am anderen Ende des Seiles würde man nur feststellen, dass dieses mit 100 N nach unten zieht, in Richtung Erdmittelpunkt. Die Zugkraft des Seiles und die Gewichtskraft der Kugel halten sich die Waage.

Komponenten einer Kraft

Befestigt man das 10-kg-Gewicht in der Mitte eines Seiles, können noch weitere Phänomene im Gedankenexperiment nachvollzogen werden. Nimmt man beide Seilenden zusammen in eine Hand und würde jetzt die Kraft an jedem Seilende ermitteln, würde man dort nur noch die Hälfte der ehemals an dem einen Seil ermittelten Kraft feststellen. Jedes Ende würde also mit 50 N nach unten ziehen. Drei Fäden würden die wirksame Kraft also dritteln – und so weiter. Ein logischer Vorgang und auf den ersten Blick langweilig. Interessanter wird dieses Experiment erst dann, wenn man die beiden Ende der Seile jeweils in eine Hand nimmt. Das angehangene Gewicht bleibt mit seiner Masse von 10 kg natürlich konstant und in der Mitte des Seiles. Damit bleibt die Art des Ziehens in Richtung Erdmittelpunkt von gleicher Größe wie bisher. An beiden Seilenden wirken 50 N senkrecht nach unten.

Aber je weiter man die beiden Seilenden nun voneinander entfernt, desto größer wird eine neue Kraft, die vorher nicht da war. Eine waagerechte Komponente schleicht sich dazu. Und je weiter man den Faden spannt, um ihn in eine waagerechte Position zu bringen, umso größer wird die waagerechte Komponente der Kraft. Ab einem Winkel der beiden Fäden von mehr als 45° überwiegt sogar die Komponente zur Seite. Wer dieses Experiment in Natur nachvollzieht, spürt diese waagerechten Kräfte deutlich. Bei einem 10-kg-Gewicht und einem dünnen Seil schneidet sich dieses bereits in die Handfläche, wenn der Winkel zum Halten etwa 120° erreicht und weiter abgeflacht wird. Das Gewicht von 10 kg konnte eben noch mit Leichtigkeit angehoben werden und jetzt wird jeder Zentimeter an Höhengewinn schwieriger und schmerzhaft in der Handfläche.

Fünf Modelle werden im Text beschrieben:

A] 10 kg Masse hängen am Ende eines Seils. Auf das Seil wirkt eine Kraft von rund 100 Newton (N)

B] Zwei Seile halten senkrecht nach oben das Gleichgewicht für die Masse. Die Seilkraft beträgt daher nur noch 50 N pro Seil

C] Die Seilenden werden voneinander entfernt. Eine waagerechte Kraft kommt dazu, die Seilkraft von zuvor 50 N erhöht sich

D] Bei einer Ausbildung eines Winkels von 45 ° entspricht die waagerechte Komponente der senkrechten. Die Seilkraft beträgt rund 71 N

E] Bei einer Spreizung von 120° für die Abspannung beträgt die Seilkraft bereits 100 N

Unendliche Weiten

Hat man ein entsprechend stabiles Seil für dieses Experiment benutzt, kann es so weit getrieben werden, dass man ein Seilende an der Wand befestigt und das andere mit aller Kraft von dieser Wand wegzieht. Ziel soll es sein, das Seil absolut in die Waage zu bringen. Es soll also durch das Gewicht von 10 kg nicht die kleinste Beule im gestreckten Seil auftreten. Schnell stellt sich dann die Frage nach der Machbarkeit – und vor allem, nach der dazu notwendigen Kraft. Nach unten bleibt die Gewichtskraft von 100 N die sich auf die beiden Seilenden zur Hälfte aufteilt. Zu den Seiten jedoch ergeben sich gänzlich andere Größen. Diese Größen wachsen mit zunehmender Anhebung des Gewichts durch das Spannen des Seiles. Was aber auch auffällt, ist die Tatsache, dass man den Faden niemals so stark spannen kann, dass dieser keine Beule mehr aufweist.

Physik und Vektoren

Dieses Phänomen lässt sich hervorragend auch zeichnerisch und daher auch mathematisch herleiten. Die Zusammenhänge und das bereits beschriebene Gedankenexperiment bieten sich an, um in die Welt der sogenannten Vektoren vorzustoßen. Vektoren haben von Haus aus einen Start- und Endpunkt sowie eine Richtung. Zeichnet man also das eben beschriebene Gewicht als Vektor für die Kraft, so könnte man im einfachsten Fall annehmen, dass die Gewichtskraft von 100N mit einer Länge von 10 cm dargestellt wird. Die Richtung ist dabei vorgegeben und klar nach unten weisend. Wenn der Faden dieses Gewicht trägt, hat er eine gleich große Gegenkraft entgegenzusetzen. Der Vektor für die Reaktionskraft des Fadens läuft also nach oben und ist ebenfalls 10 cm lang, entsprechend 100 N.

Sobald der Faden jedoch zweigeteilt das Gewicht trägt, verändern sich die Kraftverhältnisse. Die nach unten weisende Kraft des Gewichts verändert sich nicht und bleibt konstant bei dann jeweils 50 N für jedes Fadenende. Bewegt man die beiden losen Fadenenden voneinander weg, ergeben sich die bereits beschriebenen und fühlbaren Kräfte. Die Komponente mit der Drift zur Seite nimmt für das Seil zu, je weiter man die losen Enden voneinander entfernt oder anders, je flacher der Winkel. Die waagerechte Kraft ist beispielsweise bei 45° gleichwertig für den Zeiger nach unten und seinem Gegenstück zur Seite. Die Zugkraft zur Seite beträgt dann also ebenfalls 50 N. Wenn der Winkel noch flacher wird, überwiegt sogar die seitliche Komponente. Die Kraft, die das Gewicht zur Seite zieht ist dann bereits größer als die Kraft nach unten.

Das Seil selbst muss für diese Kraft geeignet sein. Und obwohl es nur eine Masse von 10 kg anhebt, kann es unter der Last aber aufgrund der Ausrichtung zu einer Überlastung und zum Reißen führen.

Vektoraddition per Faden

Die Kraft, die ein Seil aufnehmen kann, ist eindeutig eine Zugkraft längs des Seilverlaufs. Es richtet sich in die Richtung der resultierenden Kräfte aus. Es „spürt“ natürlich weder die Querkraft zur Seite noch die Gewichtskraft nach unten. Das Seil wird lediglich durch die resultierende Kraft gefordert und daher ausgerichtet. Und diese resultierende Kraft lässt sich als Addition der beiden Vektoren für die senkrechte und waagerechte Komponente addieren. Das bedeutet, der Fadenverlauf zeigt zumindest schon mal die Richtung des resultierenden Vektors an. Misst man die Komponenten bezüglich der Länge genau aus, so kann man auch auf die resultierende Kraft des Vektors schließen. Also mit der Kraft, mit der dieser Faden beansprucht wird. Würde man nun noch die maximale Kraft kennen, für die der Faden geeignet ist, so könnte man bereits eine Aussage über die Haltbarkeit dieser Abspannung treffen. So einfach kann Statik und Vektorrechnen sein.

Diese Modelle der Statik von Seilkräften lassen sich zeichnerisch und damit auch rechnerisch lösen

Beanspruchung der Punkte

Will man nun die Abspannvorrichtung mit dem Gewicht an einer Wand befestigen, so wirken auf diese Befestigung natürlich wieder die gleichen Kräfte, die auch den Faden beanspruchen. Eine Schraube würde also die Kraft nach unten und zur Seite aufnehmen müssen. Und jetzt nochmals zu dem Anspannen des Seils und damit zu der Zunahme der quer laufenden Kräfte. Je strammer man die Konstruktion spannt, umso mehr wandert der Aufhängepunkt in die Höhe und der Verlauf der Schnur nähert sich der Waagerechten.

Beobachtet man während der letzten paar Millimeter vor dem Erreichen der waagerechten Position jedoch den Vektorverlauf der waagerechten Kraftkomponente, wird dieser immer länger und läuft dann kurz vor Erreichen der waagerechten Position ins Nirwana. Der Vektor läuft dann tatsächlich ins Unendliche und trifft erst dort und nur theoretisch, den Fünfzig-Newton-Vektor für die senkrechte Komponente. Und praktisch bedeutet das, dass der Faden niemals komplett waagerecht gespannt werden kann. Die Kraft dafür lässt sich nicht aufbringen. Jeder Faden oder auch jedes Drahtseil beliebiger Dicke würde reißen. Jede Schraube, die in eine Wand fachmännisch eingedübelt worden wäre, würde unweigerlich aus dem Loch herausgerissen. Unendlich groß wäre die notwendige Kraft und damit unbezwingbar.

Dieser Beitrag ist zuerst erschienen in SBZ Monteur 06/2018.